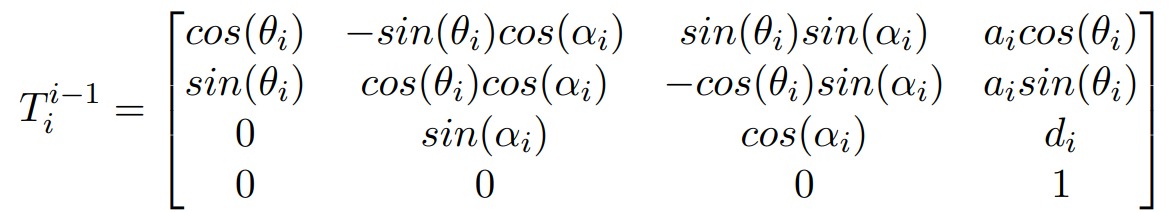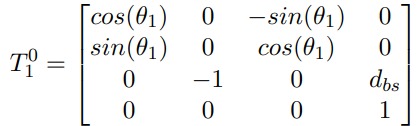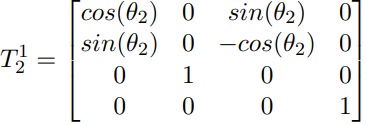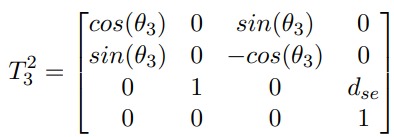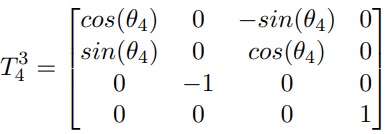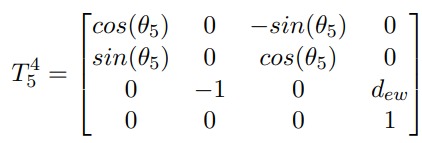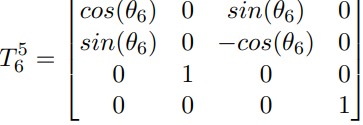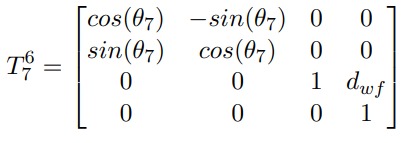Introduction
This section provides an introduction to the fundamental concepts of robotics, specifically focusing on the kinematics and control of robotic manipulators. Understanding these concepts is essential for designing and operating robotic systems efficiently.
General Terminology in Robotics (KUKA IIWA 14):
Workspace:
The reachable workspace of the KUKA IIWA 14 robot's end-effector is the manifold of reachable frames, which determines the range of motion and tasks it can perform.
Accuracy:
Accuracy on the KUKA IIWA 14 refers to its ability to position its end-effector precisely at a desired target point within the work volume, influenced by factors such as sensor technology and control algorithms.
Repeatability:
Repeatability on the KUKA IIWA 14 is a measure of its ability to consistently return to a specific position when performing repetitive tasks under similar conditions. It is crucial for maintaining precision and reliability in industrial applications.
Safety:
Ensuring safety is paramount in the design and operation of the KUKA IIWA 14. Its collaborative features and advanced control systems aim to minimize the risk of human-robot collisions and ensure a safe working environment for human-robot interaction.
Advanced Algorithm Description :
Advanced algorithms for robotic manipulators include various techniques for optimizing motion planning, trajectory planning, and adaptive control.
These algorithms enhance the performance and efficiency of robotic systems, enabling them to handle more complex tasks and operate in dynamic environments.
Particle Swarm Algorithm :
PSO is a population-based stochastic optimization technique inspired by the social behavior of birds flocking or fish schooling. In PSO, a population of potential solutions (particles)
is initialized randomly, and these particles move through the search space, adjusting their positions based on their own best-known position and the global best-known position of the entire swarm. This movement is guided by mathematical formulas derived from the behavior of social groups.
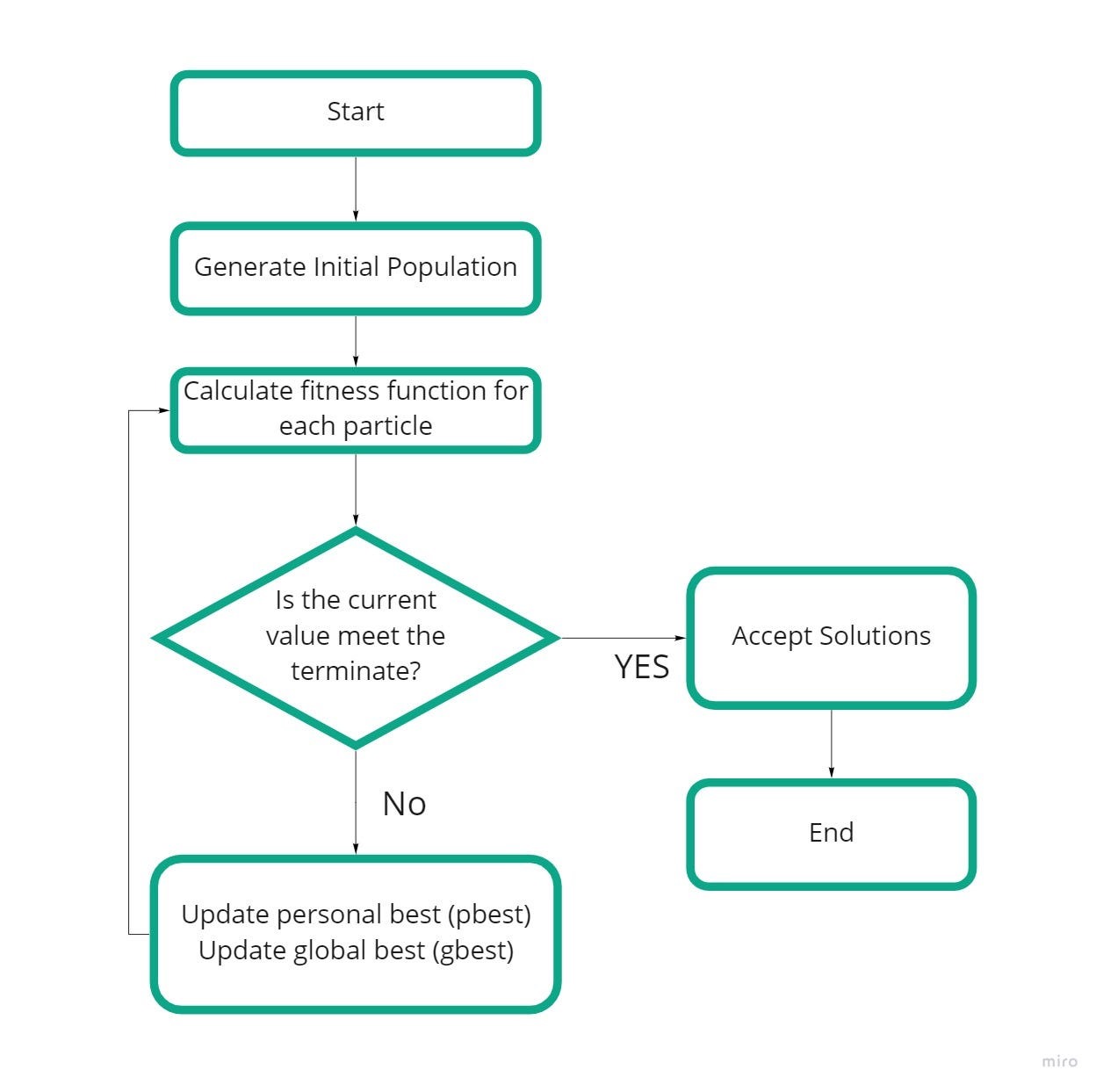
PSO can be applied to solve various optimization problems, such as inverse kinematics (IK). Inverse kinematics is the process of determining the joint configurations of a robot to achieve a desired end-effector position. PSO can be used to search for optimal
joint configurations that minimize the difference between the desired end-effector position (target position) and the actual end-effector position. By using PSO, the robot can efficiently explore the joint space and find solutions that satisfy the given constraintsand objectives.
PSO is used to solve the inverse kinematics problem for a robotic manipulator (represented by the imported robot model). PSO is compared with another method, Jacobian-based IK, to evaluate its performance in terms of accuracy and computation time.
Analysis :
When to Prefer PSO for Inverse Kinematics:
1. Highly Nonlinear Systems:
PSO: Effective for highly nonlinear systems where the relationship between joint angles and end-effector position is complex.
Jacobian: May struggle with convergence if the system is highly nonlinear and if the Jacobian matrix is difficult to compute or becomes singular.
2. Discontinuous or Non-Differentiable Objective Functions:
PSO: Does not require the objective function to be continuous or differentiable, making it suitable for problems where the objective function has discontinuities or is not differentiable.
Jacobian: Requires the objective function to be smooth and differentiable to compute gradients.
3. Global Optimization:
PSO: Capable of global search and can avoid getting trapped in local minima, making it suitable for finding global solutions in complex search spaces.
Jacobian: Primarily a local search method, which can get stuck in local minima and may not find the global optimum.
4. Complex Constraints:
PSO: Handles complex constraints naturally, as it evaluates the fitness of each particle considering all constraints.
Jacobian: Handling complex constraints may require additional modifications or constraints handling techniques.
5. Initialization Sensitivity:
PSO: Less sensitive to initial conditions due to its population-based nature, which explores multiple regions of the search space simultaneously.
Jacobian: Highly sensitive to initial conditions, and poor initialization can lead to slow convergence or failure to converge.
Frequently Asked Questions
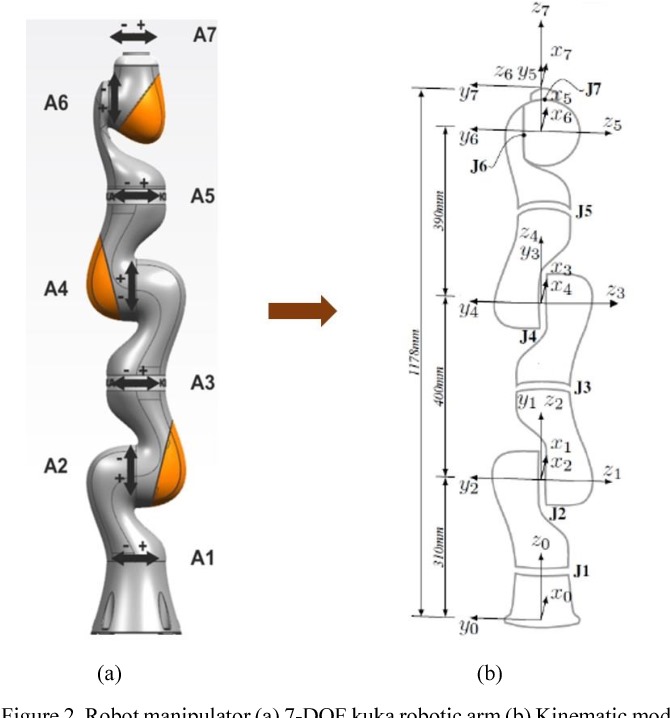
Explain the significance of Degrees of Freedom (DOF) in a 7DOF manipulator.
The Degrees of Freedom (DOF) in a 7DOF manipulator refer to the number of independent movements the manipulator can make. With 7 DOF, the manipulator has more flexibility and can perform complex tasks that require precise positioning and orientation in 3D space.
What are the common manipulator types in 7DOF systems?
Common types of manipulators in 7DOF systems include articulated robots, which use a series of rotary joints, and anthropomorphic robots, which are designed to mimic the human arm. These configurations allow for versatile movement and control.
Why is the Jacobian matrix important in the analysis of a 7DOF manipulator?
The Jacobian matrix is crucial for analyzing a 7DOF manipulator as it relates the joint velocities to the end-effector velocities. It helps in understanding the manipulator's kinematics and is essential for motion control and stability analysis.
What role do joint angles play in the control of a 7DOF manipulator?
Joint angles determine the position and orientation of the end-effector in a 7DOF manipulator. Controlling these angles precisely is vital for achieving the desired end-effector position and performing tasks accurately.
Describe the concept of workspace for a 7DOF manipulator.
The workspace of a 7DOF manipulator is the volume of space within which the end-effector can move and operate. It is determined by the manipulator's geometry and joint limitations, and it defines the range of tasks the manipulator can perform.
How does inverse kinematics differ from forward kinematics in the context of a 7DOF manipulator?
Inverse kinematics involves calculating the joint parameters required for a desired end-effector position, while forward kinematics involves determining the end-effector position from given joint parameters. Inverse kinematics is more complex and crucial for precise control.
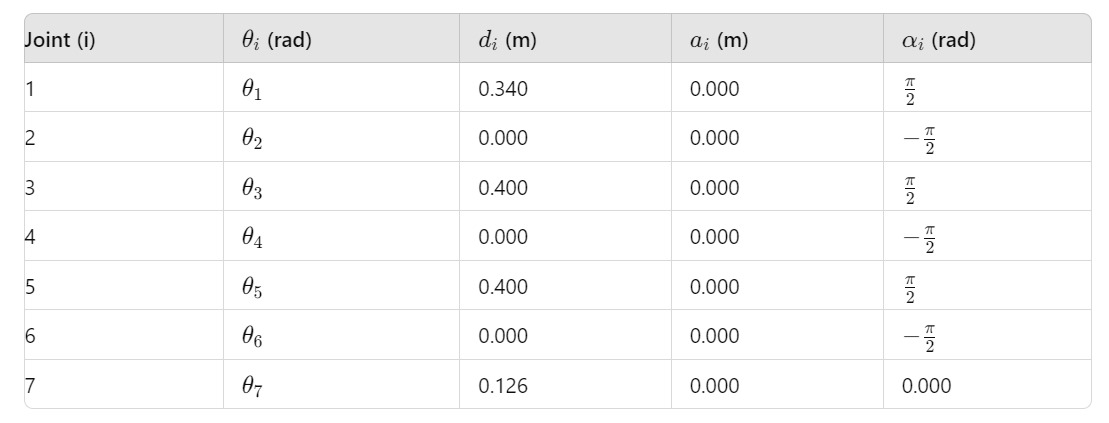
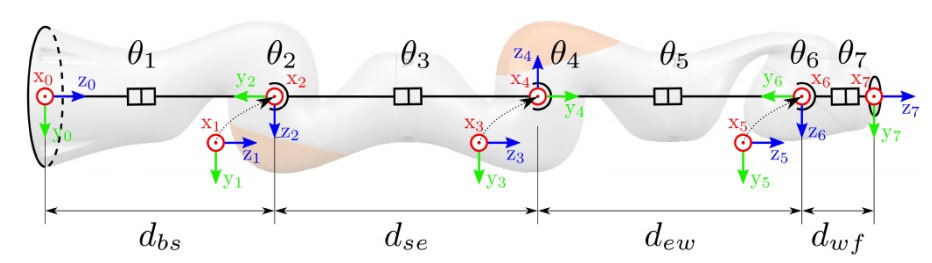
What is the Denavit-Hartenberg (D-H) parameterization and how is it used in modeling a 7DOF manipulator?
The Denavit-Hartenberg (D-H) parameterization is a standardized method for representing the kinematic chains of robotic manipulators. It simplifies the modeling process by defining a set of parameters that describe the relative positions and orientations of adjacent links.
How do singularities affect the operation of a 7DOF manipulator?
Singularities in a 7DOF manipulator occur when the Jacobian matrix loses rank, leading to a loss of one or more degrees of freedom. This can result in uncontrollable or unpredictable behavior, making certain positions and orientations unattainable or requiring infinite joint velocities.